How bar model drawing techniques improve overall math performance

Wiki Article

Exploring Bar Model Drawing Techniques: A Comprehensive Guide to Imagining Mathematics Concepts

Bar version attracting strategies act as a valuable resource for both educators and trainees in picturing mathematical ideas. These designs simplify complex numerical relationships, aiding in the comprehension of enhancement, subtraction, department, and reproduction. This guide describes effective approaches for applying bar designs, promoting energetic interaction and real-world connections. As readers discover the functional applications and training ideas, they will certainly discover exactly how these methods can transform their strategy to maths.

Understanding the Essentials of Bar Model Drawing

Bar design attracting functions as a powerful visual tool in maths, assisting in the understanding of numerical partnerships and problem-solving strategies. This technique entails representing numbers and their partnerships with rectangular bars, making it easier to picture operations such as enhancement, division, multiplication, and subtraction. Each bar's size represents a specific value, enabling students to contrast amounts and comprehend percentages plainly.

To develop a bar design, one starts by determining the issue's key elements, often breaking it down into components that can be aesthetically represented. For instance, in a straightforward addition issue, two bars can be drawn, with their lengths standing for the addends. The combined length highlights the amount. On top of that, bar designs can be adjusted for more complex troubles, including ratios and portions, by changing benches as necessary. Mastering these fundamentals lays a strong structure for efficient analytic and deeper mathematical understanding.

Benefits of Utilizing Bar Designs in Math

Using bar designs in mathematics provides various advantages that enhance discovering and comprehension. These graphes help trainees in comprehending complicated principles by damaging them down right into manageable components. Bar designs provide a clear structure for showing connections between numbers, making abstract ideas much more concrete. They advertise a much deeper understanding of mathematical operations and facilitate analytic by allowing learners to imagine the data they are dealing with.

Furthermore, bar models sustain the advancement of important believing skills, as trainees should analyze and analyze the visual information to reason. This method motivates energetic engagement with the product, reinforcing retention and proficiency of mathematical principles. By cultivating a strong structure in visual literacy, bar versions equip learners to approach numerous mathematical challenges with confidence. On the whole, the integration of bar designs right into maths education verifies valuable in growing both comprehension and logical abilities amongst students.

Applying Bar Versions to Enhancement and Reduction

Bar versions work as a reliable device for visually representing addition and subtraction problems. By illustrating the partnership in between numbers, they enhance understanding and facilitate analytical. Furthermore, real-life applications of these versions can aid learners comprehend mathematical principles in functional contexts.

Standing For Addition Visually

When pupils encounter enhancement and subtraction problems, aesthetic aids can considerably improve their understanding of these operations. Bar designs serve as effective devices for standing for addition. By dividing a rectangular shape into segments that represent the numbers included, students can visualize the connection between the amounts. If a student requires to include 3 and 5, they can develop a bar divided right into two areas: one section standing for 3 and the various other representing 5. This clear representation not only streamlines the enhancement process yet also enhances the concept of combining quantities. As pupils adjust these visual aids, they establish a deeper comprehension of addition, causing boosted problem-solving abilities and greater self-confidence in their mathematical capabilities.

Subtraction With Bar Versions

Although subtraction is usually viewed as an extra complex operation than enhancement, bar versions can effectively clarify this procedure for pupils. By visually representing the amounts involved, students can much better understand just how numbers connect to one an additional. In a bar design for reduction, one bar stands for the total, while another suggests the quantity being subtracted. This aesthetic distinction helps trainees comprehend the concept of "removing." If a bar shows 10 devices, and an additional bar standing for 4 devices is removed, trainees can conveniently see that 6 devices continue to be. This technique not just fosters understanding of reduction yet additionally help in developing analytical skills, allowing trainees to picture their mathematical thinking and improve their general understanding of mathematical principles.

Real-Life Application Instances

Understanding subtraction with bar designs lays a foundation for using these strategies in real-life scenarios. In numerous contexts, such as budgeting or buying, people can visualize just how much cash remains after expenditures. If an individual has $50 and spends $20, a bar design can represent the complete amount and the spent portion, highlighting that $30 is left. In addition, parents can use bar designs to aid kids understand how lots of more things require to be added to finish a set, such as having three apples and needing 5. This visual representation simplifies complex troubles, assisting in comprehension and retention. Inevitably, bar designs work as effective tools in everyday decision-making, enhancing mathematical understanding in sensible scenarios.

Picturing Multiplication and Division With Bar Designs

In checking out the application of bar designs for reproduction and division, it is necessary to comprehend their foundational principles. Building multiplication designs enables learners to envision relationships between numbers, while efficient division methods can be highlighted through these aesthetic aids. This approach enhances comprehension and problem-solving abilities in maths.

Comprehending Bar Designs

Bar models act as an effective aesthetic device for illustrating the concepts of multiplication and division. They make it possible for learners to represent mathematical connections in a structured layout, helping with a much deeper understanding of these operations. In multiplication, bar designs show teams of equivalent dimension, allowing people to picture the total amount when integrating these teams. On the other hand, in division, bar designs aid portray how a total amount is divided into smaller, equal components, clarifying the idea of partitioning. By utilizing these visual help, students can realize the underlying concepts of reproduction and division much more properly. This approach not just boosts comprehension but additionally supports problem-solving abilities, making bar designs an invaluable asset in mathematical education.

Creating Multiplication Designs

Constructing multiplication designs using bar diagrams provides a clear method for picturing the process of multiplication. These designs make it possible for students to represent reproduction as teams of equivalent parts, making abstract concepts extra concrete. To show (3 times 4), a student can attract one bar divided right into 3 equivalent sections, each representing 4 systems. In addition, creating a 2nd bar with the same size enhances the understanding of duplicated enhancement, as each segment represents one group. This graph not just aids in comprehending multiplication but likewise enhances problem-solving skills. By utilizing bar models, pupils can better comprehend connections between numbers and create a robust structure for more complex mathematical concepts, causing enhanced confidence in their capacities.

Picturing Department Methods

While multiplication commonly gets the limelight in very early mathematics education and learning, department is similarly essential and can be effectively envisioned using bar versions. Bar models offer a clear visual representation of department troubles, damaging down the process into convenient components. For circumstances, when splitting a total amount into equivalent groups, students can draw a lengthy bar to stand for the entire and then segment it into smaller bars that indicate each group. This method not only illustrates the principle of equivalent sharing yet additionally enhances the connection in between reproduction and department. By making use of bar models, students can much better understand department as a process of dividing, helping to strengthen their understanding of this basic mathematical procedure.

Addressing Word Troubles Utilizing Bar Version Techniques

Exactly how can visual depictions enhance the understanding of word troubles? Bar design techniques give a powerful tool for students to damage down intricate scenarios into convenient parts. By translating words right into aesthetic bars, learners can identify connections in between quantities and operations more easily. Each bar stands for a specific value, allowing students to see how various elements of the problem connect.

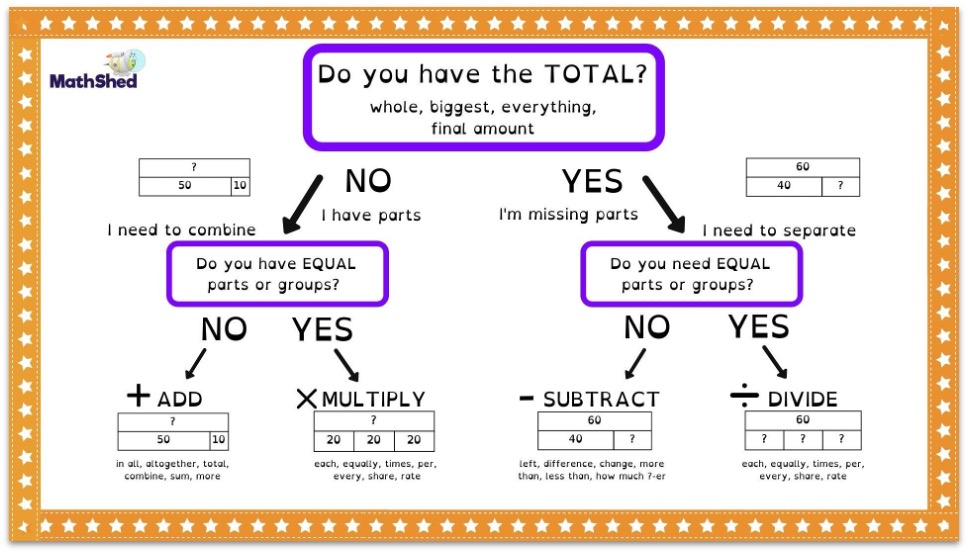
For example, in an issue entailing enhancement and subtraction, pupils can draw separate bars for each quantity and afterwards adjust them to find the option. This procedure not only makes clear the issue however also cultivates a deeper conceptual understanding. In addition, bar designs can be adjusted for different kinds here of word problems, making them functional across different mathematical topics. Ultimately, utilizing bar designs can significantly improve pupils' analytical skills by offering a clear visual pathway to get to the proper solution.

Integrating Bar Versions in Different Math Topics

Bar models can be flawlessly integrated right into different mathematics subjects, improving pupils' understanding of principles beyond basic math. In algebra, these visual tools help in representing inequalities and equations, allowing learners to picture partnerships in between variables. When tackling geometry, bar designs can show the properties of forms and spatial thinking, assisting trainees comprehend concepts like area and border effectively. In stats, bar models facilitate the interpretation of data collections, allowing trainees to compare quantities and recognize trends visually. Additionally, integrating bar versions within dimension topics help in recognizing units and conversions by offering a concrete depiction of quantities. By employing bar designs across different mathematical areas, instructors can foster a much deeper understanding of complex concepts, thereby improving problem-solving abilities and promoting important reasoning (bar model drawing techniques). This adaptability demonstrates the energy of bar designs as a foundational tool for students in their mathematical trip

Tips for Teaching Bar Designs Efficiently

Incorporating bar models right into mentor practices requires thoughtful approaches to optimize their efficiency. Educators must begin by introducing bar versions with simple, relatable examples that pupils can quickly understand. This aids to develop confidence and knowledge with the principle. Gradually raising the complexity of troubles permits learners to use their skills progressively. Furthermore, teachers need to motivate pupils to create their very own bar designs, promoting energetic interaction and ownership of their knowing.


Incorporating collective activities can likewise boost understanding, as pupils go over and address issues in teams. Constant comments is essential; instructors ought to supply positive discourse on pupils' bar version depictions to assist enhancement. Attaching bar versions to real-life circumstances strengthens their significance, assisting pupils see the practical applications of their mathematical abilities. By carrying out these approaches, teachers can effectively harness the power of bar models in their mathematics instruction.

Frequently Asked Inquiries

Can Disallow Models Be Utilized in Other Subjects Besides Mathematics?

Bar models can indeed be utilized in various subjects past mathematics. They effectively illustrate concepts in science, social studies, and language arts, helping to visually stand for connections, processes, and ideas for enhanced understanding across techniques.

What Age Group Is Best Suited for Knowing Bar Designs?

Bar models are best suited for children ages 7 to 12, as they develop concrete thinking skills during this duration (bar model drawing techniques). At this age, pupils can effectively grasp abstract ideas with graph and problem-solving methods

Exist Digital Devices for Creating Bar Versions?

Yes, numerous electronic tools exist for developing bar designs, consisting of educational software application and online systems. These devices help trainees visualize mathematical concepts efficiently, improving their understanding and interaction in discovering through interactive and dynamic representations.

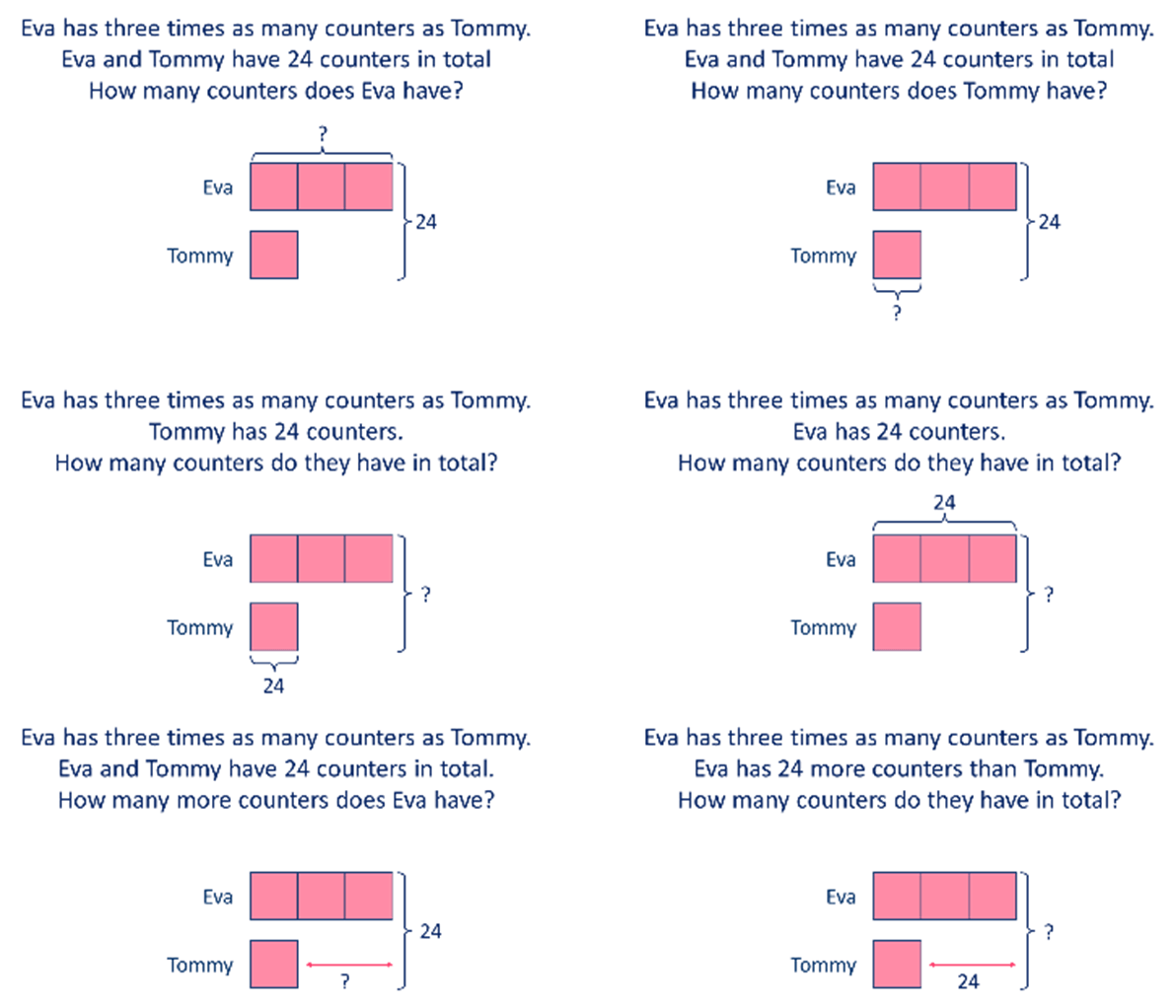
Exactly How Can I Evaluate Trainee Understanding of Bar Designs?

Evaluating pupil understanding of bar versions can entail tests, observational evaluations, and seminar. Educators may likewise evaluate students' finished versions and their capability to clarify their thinking, making sure a detailed assessment of understanding.

What Are Common Errors When Utilizing Bar Versions?

Common errors when using bar designs include misrepresenting quantities, failing to precisely identify bars, puzzling enhancement and reduction, disregarding to make use of constant ranges, and overlooking the significance of clear visual separation between different aspects.

In enhancement, bar models can be adapted for more complicated issues, consisting of portions and ratios, by changing the bars as necessary. Subtraction is often viewed as an extra complex procedure than addition, bar versions can properly clarify this procedure for pupils. In a bar model for reduction, one bar stands for the total, while one more shows the amount being subtracted. If a bar reveals 10 devices, and another bar standing for 4 devices is removed, trainees can conveniently see that 6 devices remain. When dividing an overall right into equivalent teams, students can draw a long bar to stand for the whole and after that segment it into smaller sized bars that indicate each team.

Report this wiki page